Основната основа за всички учения, които познават света, е математика. Точната наука използва формализиран език и изучава ред, структура и взаимоотношения върху избрани абстрактни обекти. Не всички учащи харесват математиката заради нея сложност и объркване, но най-вероятно защото недоразумение. Продължителните промени във връзка с математиката ще изискват отдаденост, концентрация, последователност, дори упоритост и най-важното - практически решения. В проучването е важно стъпка по стъпка да разберем първоначално простото и постепенно да преминем към по-сложното, без да оставяме нищо неразбираемо и немислено.
Има много различни клонове на математиката, които са достатъчно изучени и се появяват наскоро. По-долу са описани основите на математическия анализ - основните начални понятия, дефиниции и правила за изучаване на прости функции на една променлива, производна и диференциация.
Афоризмът възникна сред учениците в началните класове: "Математиката става наистина сложна, когато числата изчезнат от нея." Всъщност те се доближават до разбирането на някои от определенията и законите на математическата наука, като решават правилата, като използват конкретни примери..
Основни определения
Да започнем с терминологията - с прости общи семантични значения на основните дефиниции:
- променлив - стойност или символ, може да вземе някоя от редица стойности в
конкретна площ (тегло или височина на детето)
- функция - цел, работа, дейност, специфично действие върху променлива, обозначаваме f (x) (зависимостта на теглото на детето от неговия ръст)
- лимит - граница, граница, ръб (хоризонт - зрително поле)
- дериват - образувани, вторични, изтичащи от друг, обозначаваме f '(x) (скорост при движение)
- диференциал - разлика, разграничение, раздяла.
Функцията е просто
Функцията е резултат от това, което прави с променлива, която е резултат на изчисление. Това е отношение на елементи, при което промяна в една променлива предизвиква промяна в друга. Разделете f (x) на прости и сложни.
Следните методи се използват за показване на зависимости: алгебрични, графични, таблични, логически и дори софтуерни.
Числовите зависимости се определят алгебрично с помощта на символите на променливи, равенства и неравенства (≤ и>), се изгражда уравнение на формата: y = f (x), тук x е променлива или аргумент, а y или f (x) е функция. За всяка конкретна стойност на променливата x от допустима област на дефиниране съответства определена стойност на y за даден f (x).
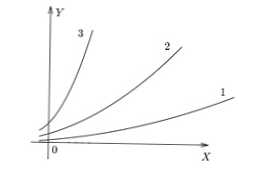
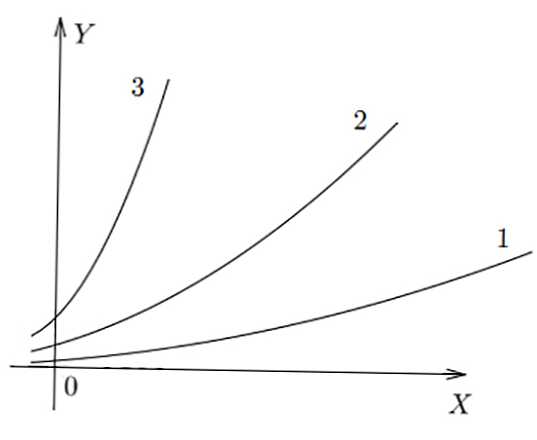
Фигурата по-долу показва прости графики с 3 различни съотношения. Вижда се, че в f (x) 3 най-голямата стойност на y се получава за x специфична, в f (x) 1 - най-малката.
функция
Различават се следните елементарни изрази: линеен (директен), квадратичен (парабола), кубичен, хипербола, експоненциален, логаритмичен, тригонометричен (показан в таблицата по-долу).
За анализа на всеки тип f (x) се определят присъщите им свойства (изброени по-долу), за това се използват понятията производни и диференциали.
Производна функция
дериват - оператор, което за оригиналното f (x) според законите на диференциацията свързва друга функция, тя характеризира промяната в основния f (x) на аргумента x в някакъв момент. За подробно разбиране на това, трябва да се справим с по-сложни дефиниции на границата на зависимостта и диференциацията..
лимит - това определение е динамично. Изразът, който x има тенденция към n, се разбира по следния начин: x придобива стойности, близки до n и се различават с малко количество.
диференциал - малка промяна в някаква величина. Прирастът се нарича делта.
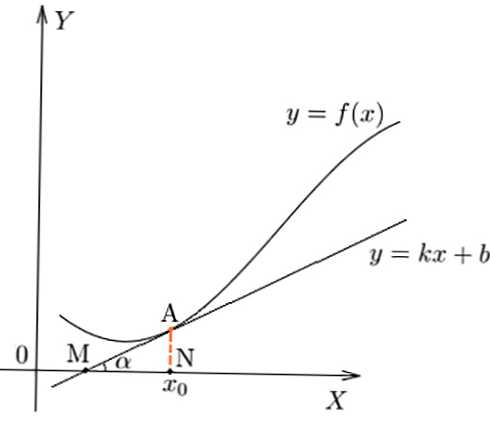
Производната за f (x) в точка е границата на разделяне на делта на функцията на делта на променливата в дадена точка, ако последната има тенденция към 0.
Характеристиката на скоростта на промяна на зависимостта в дадена точка, геометрично тя може да бъде показана като стойността на тен на ъгъла на наклона на алфа допирателната към функцията.
дериват
Зависимостта се нарича диференцируема, ако е дефиниран f '(x). Намирането на производно се нарича диференциация. Правилата за изчисляване на f '(x) и съвпадение на f' (x) от елементарни f (x) са дадени в таблицата по-долу
Извлечената функция също функционира
Всяка зависимост има определени свойства, знаейки и изследвайки ги можете да анализирате естеството на състоянието и промените f (x).
Основни свойства:
- Данни за дефиниция и стойност на разликата.
- Нула f (x)
- Функцията се увеличава или намалява в някои интервали.
- Посочва MAX и MIN функции, има ли наклон.
- Нечетно или нечетно f (x)
- Ограничена и неограничена функция.
- Има ли асимптоти.
- Честота f (x).

Функции и производни
При установяване на характеристиките на зависимостта с помощта на производната се използват взаимовръзки на свойствата f '(x) със свойствата f (x) и обратно. Характеристиките f '(x) лесно се определят на графиката на функциите и обратно, характеристиките на първичното f (x) се разбират от графиката f' (x). Фиксирайки същността на всяка характеристика на функцията, проучете и установете верига от взаимоотношения. За определяне на асимптотите в графики се използва понятието граници..
По-долу са някои характеристики и зависимости на f '(x) от f (x):
- Тъй като f (x) се увеличава в интервала, f '(x) е положителен.
- Ако f (x) намалява през интервала, f '(x) е отрицателен.
- При наличието на f (x) точката MAX, f '(x) = 0 в нея може да не бъде определена и tg на тангенсния ъгъл се променя от + на -.
- При наличието на f (x), точката MIN, f '(x) = 0 в нея може да не бъде определена, а tg на ъгъла на тангента се променя знак от - на +.
- При огъване на f (x) в Е, стойността f '(x) не променя знака в точката, f' (x) = 0.
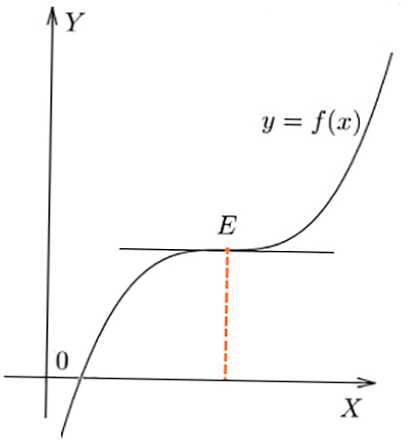
Преклонение в точка E на графиката на функциите
За изследвания f (x) съставят схема, при която всяка стъпка е конструирана според специфичен алгоритъм за изчисляване и анализ на връзките на компонентите на компонента.
Разлики във функция и производни
Правилата на събиране и изваждане f (x) са същите като правилата на тези действия по време на диференциация. Но правилата за намиране на f '(x) под действията на умножение и деление на функции са различни (както е в таблицата).
Функцията е първична, а производната е вторична математическа операция; в повечето случаи те имат различни характеристики.
Точката на преглъщане на непрекъсната зависимост се намира от втората й производна, знакът й трябва да се променя в областта на точката x0.
Има такива видове функции, които нямат f '(x) в точката x0 (прекъснато). В израз ln (| x | -1) производната не е дефинирана в точката x0 = 1.
Има изрази "Modulo" подобно на y = | x |, което има отклонение в x0.
За такива зависимости се използват само частично (на интервалите на дефиниционната област) методи за изучаване на техните свойства с помощта на производни и не винаги е възможно да се премине от свойствата f '(x) към свойствата на първичната.
Никъде не може да се направи без изключения от правилата и дори в математиката. За да се анализира и консолидира представеният материал, е наложително да се решат примери, да се практикува, да се натрупа опит с ограничения, диференциали и производни и смело да се премине към интеграли.











